有理数和无理数学的区别

有理数和无理数是初中七年级比较重要的概念，也是同学们在学习过程中难易理解和掌握的知识点。本文主要从有理数和无理数的概念，来说明有理数和无理数的区别。

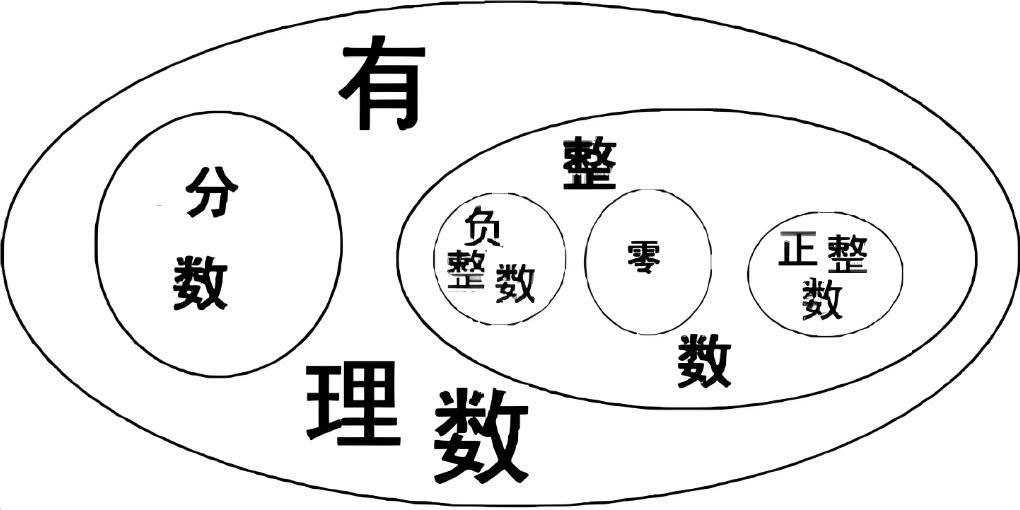
一、什么是有理数

有理数是指可以表示为两个整数的比值的数，即形式为 a/b 的数，其中 a和 b都是整数，并且 b≠0。有理数包括整数（如 −3,0,7）、有限小数（如 1.25）、和无限循环小数（如 0.333…）。

有理数的一个显著特点是，它们可以通过分数来表示。也就是说，无论这个数有多大或者多小，只要能用两个整数的比值来表示，它就是有理数。例如，0.75 可以写成 3/4，因此 0.75 是有理数。

二、什么是无理数

无理数是指不能表示为两个整数的比值的数。换句话说，无理数无法用简单的分数形式来表示。这类数包括无限不循环小数，例如 π（圆周率）和 根号2（2 的平方根）。

无理数在现实生活和数学研究中有着重要的应用。例如，π用于计算圆的周长和面积；当两个直角边的长度都是 1 时，根号2是直角三角形斜边的长度，

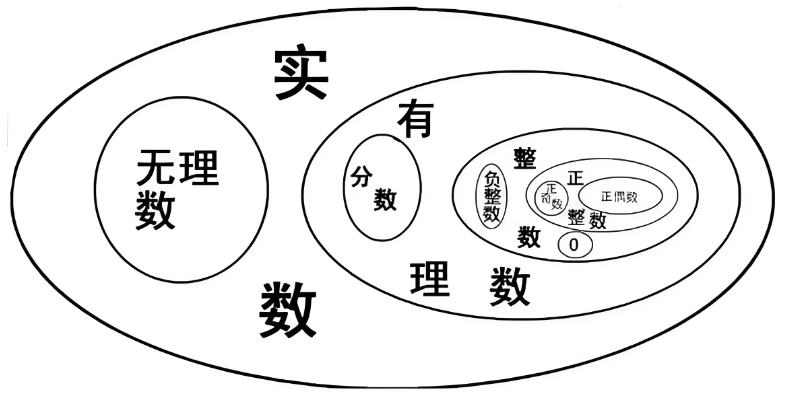
三、有理数和无理数的区别

有理数和无理数是实数的两个子集，它们有着明显的区别：

1. 表示方式：有理数可以表示为分数 a/b（a 和b 是整数，且b≠0），而无理数无法表示为分数。
2. 小数表示：有理数的小数表示形式可以是有限小数或无限循环小数，而无理数的小数表示形式是无限不循环小数。
3. 例子：有理数的例子包括 2,−5,0.75,0.666…；无理数的例子包括 π,e（自然对数的底数）。
4. 存在性：在数轴上，有理数和无理数是相互交织的。无论有理数如何密集，总能找到无理数之间的间隙。反之亦然。

通过对有理数和无理数的深入了解，我们不仅能够更好地掌握基础数学知识，还可以在解决复杂数学问题时更加游刃有余。这篇文章旨在帮助您清晰地理解两者的定义及其区别，从而在数学学习和应用中获得更多的自信和乐趣。