高清初一数学有理数知识点总结思维导图

初一数学有理数

在初一的数学学习中，有理数是一个重要的基础概念，它不仅是后续数学知识学习的基础，更是培养学生逻辑思维和问题解决能力的关键。本文将带领大家一同探索有理数的奥秘，帮助大家轻松掌握这一知识点。

一、有理数的定义与分类

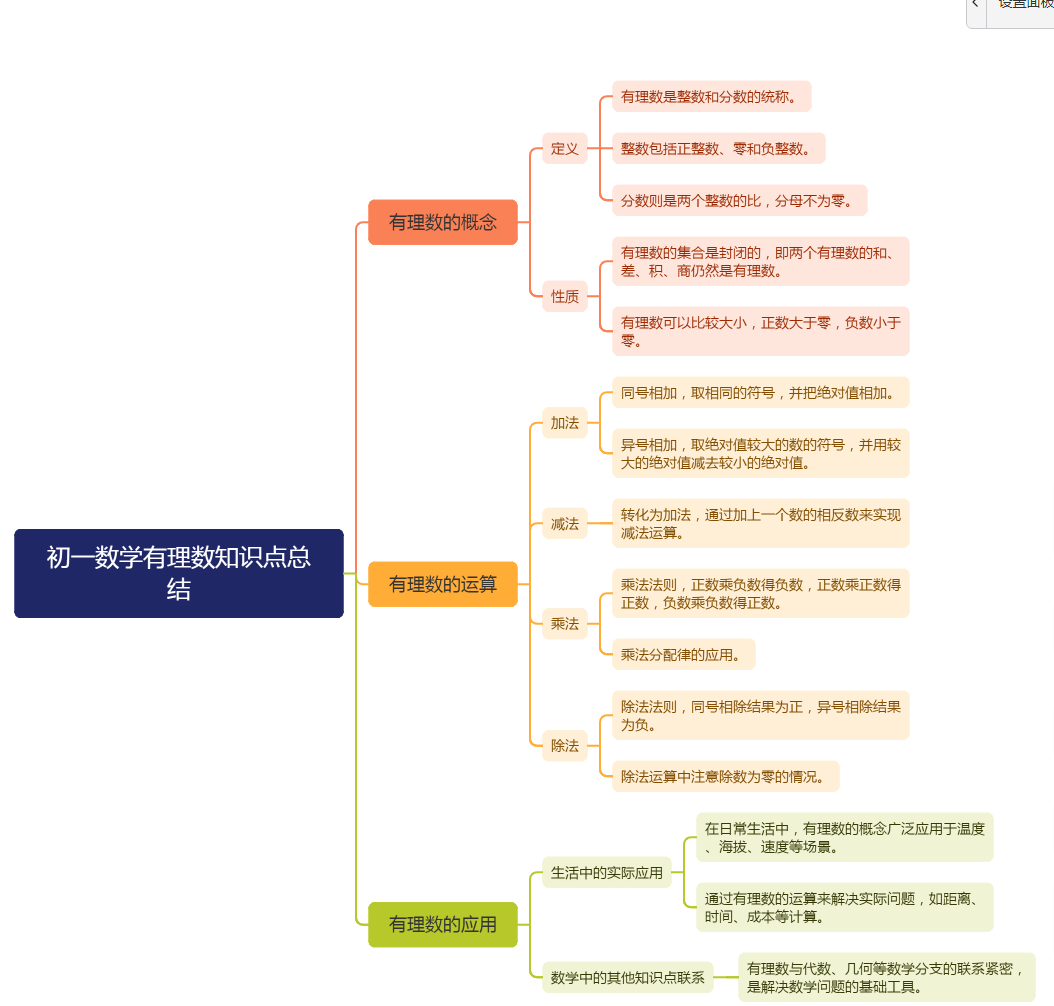
有理数，顾名思义，就是可以表示为两个整数之比的数。具体来说，有理数包括正整数、零、负整数、正分数和负分数。我们可以将其按照正负性质进一步分为正有理数、零和负有理数三类。正有理数大于零，负有理数小于零，而零则位于中间，是唯一的非正非负的有理数。

二、有理数的运算

有理数的运算包括加法、减法、乘法和除法。在运算过程中，我们需要遵循一些基本的运算法则，如加法交换律、结合律，乘法交换律、结合律和分配律等。同时，我们还需要注意运算的优先级，即先乘除后加减，有括号先算括号内的运算。

在有理数的运算中，特别需要注意的是负数的运算。负数的加法可以理解为减去一个正数，而负数的乘法则遵循“同号得正，异号得负”的规律。此外，我们还需要掌握有理数的绝对值概念，它表示一个数在数轴上离原点的距离，对于理解有理数的性质和运算有着重要作用。

三、有理数在实际生活中的应用

有理数不仅仅是数学中的一个概念，它在我们的实际生活中也有着广泛的应用。比如，在温度的测量中，我们经常使用到有理数来表示温度的高低；在海拔的测量中，有理数也被用来表示地面以上的高度和地面以下的深度；在购物时，我们也需要使用有理数来进行价格的计算和比较。因此，掌握有理数的知识点不仅有助于我们更好地学习数学，还能帮助我们更好地理解和解决生活中的问题。